Dividing a Circle

I came across this item (https://www.loc.gov/resource/g3200m.gcw0013960/?sp=9) from an online copy of the 1862 Johnson's new illustrated family atlas.  The picture intrigued me for lots of reasons, but the one that stuck in my head was the fact that it shows a circle divided into nineteen equal sectors.  That's pretty remarkable, since the 360 degrees in a circle are not nicely divided into 19 equal pieces, and I did not think 19 pieces was one of the divisions possible using compass and straightedge constructions.  (I checked; it isn't.)

I wondered how the draftsperson who created the image divided the circle?  Protractors have been around for centuries, so it is possible that they simply measured the necessary angle with a protractor.  I wasn't satisfied with that, because it seems not quite precise enough.  One would need a really carefully scaled protractor to measure an angle of just under 18.95 degrees.  Maybe the draftsperson just used 19 degrees?  After all, 19 sectors at 19 degrees each would be 361 degrees, which at the scale of the drawing might have been accurate enough.  So maybe they did use a protractor.

But I wanted something precise and elegant.  Something that could be done simply, and would provide an accurate division of the circle, without losing even a fraction of a degree.  And if the process were scalable to divide the circle into any number of sectors, that would be the icing on the delicious mathematical cake.  I had not seen such a process or tool, but its existence seemed possible and even reasonable, even if not with a compass and straightedge.

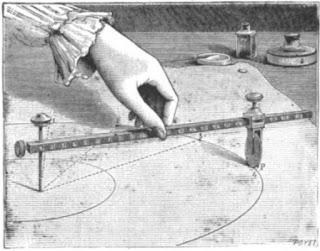
After some searching, I found an amazing device called ... get ready for it ... the Circle-Divider! (https://babel.hathitrust.org/cgi/pt?id=uiug.30112037739783&view=1up&seq=220&skin=2021).  The article in an 1885 issue of Scientific American Supplement even used 19 divisions as an example. 

The basic idea uses a small wheel with radius of one unit attached to the end of an adjustable arm, so that it could roll around the perimeter of a circle with radius n units.  (It doesn't matter what units we use, as long as they are the same for the wheel and the rotating arm.)  A mark would be positioned at the bottom of the wheel, and the arm would be rotated around the center of the radius n circle, with the wheel rolling along the perimeter.  Each time the mark on the wheel reaches the lowest point, you can mark that position on the circle, and after one rotation, the circle is divided into n sectors!  (And I love that the illustration shows what appears to be a woman's hand using the device.)

This was beautiful and simple!  All it uses is the formula for circumference, which middle school students typically know.  Since the circumference of the circle on the paper is 2pi times its radius, n, and the wheel has circumference 2pi, the wheel will rotate exactly n times as it rolls around the perimeter of the circle.  (And if your circle divider draws a 19-inch circle with 19 sectors, but you want a five-inch circle with 19 sectors, just make your smaller circle concentric with the larger one, and the sectors you want will match with the sectors you have.)

It's not a traditional compass and straightedge construction, but awfully close!  No need for a ruler (since you can construct a segment n units long, given the length of one unit).  The result is theoretically exact.  And the process is scalable to any size circle with any number of sectors!  This is what I consider a precise and elegant solution to the problem.

Here's the difficulty ... I have not been able to find this tool referenced anywhere but in this short Scientific American article about it.  And the only name I have is "circle-divider" from that article.  It's not part of a typical drafting toolkit, either modern or 19th century as far as I can tell.  A librarian from the Science, Technology, and Business Reading Room at the Library of Congress is helping me track it down, but neither of us has found another reference so far.

I'm not sure if I'm hoping to be able to find an actual circle-divider (I love old tools), or if I'm more excited to actually build one (I've got plenty of cardboard and other scraps around).  Either way, the circle-divider will certainly be making an appearance in my Trig/PreCalc class next year!