Rollercoasters Are Scary!

The other day, I was giving my midyear presentation for the Einstein Fellowship, and talked about how I filter everything I do and learn through the lens of going back to the classroom.  I know that's where I belong, teaching math to students is what I do best, and watching them grow personally and mathematically is what I enjoy.

HOWEVER ...

As much as I am excited to go back to the classroom in August, I am just as afraid.  I won't have been in front of a class of students in over two years, thank you not at all, covid.  My experience as a Fellow has been so different from the experience of my colleagues, and even more so, as they've taught remotely, in a hybrid setting, and with masks on every day.  That's a situation that can bind people together, and I'm not there.  Additionally, my school has switched from a nine-period-a-day, 42-minute class period schedule to a block schedule with 85 minute periods.  The closest I've been to a block schedule is teaching summer school.  Also, I think two of the courses I have most recently taught have gone through some curriculum changes, and I think the third is in process.

The upshot is that at an age where I should probably start thinking seriously about retirement, I will most likely feel like a brand new teacher all over again.  That scares me; that's a discomfort I've not felt in a long time.  And it's a feeling I've been missing.  I applied for the Fellowship to shake me up a bit.  Well, I've been shaken, stirred, spun around, and turned upside down the last two years, and it's been great.  So while the roller coaster I'm going to be on next year will be familiar in some ways to the one I left two years ago, there will be new twists, unexpected drops, and exciting turns.  It's going to be scary.

And it's going to be fun.

Photo by Ittsky from pixabay.

Remember ...

Since I started teaching umpteenish years ago, I have only been out of the classroom for six years.  First, when I took off a year to start my Masters degree, then three years as Department Chair, and now two years working on a Fellowship with the Library of Congress.  Being outside the classroom this time has allowed me to really indulge my curiosity and flex my writing muscles in ways I never have before, and I'm always happy to share what I learn with others.

This week, I've been working on a webinar that a colleague and I are making about teaching with primary sources.  We presented our draft to another team member, who asked at the end, "So, what does this look like in your classroom?  What advice do you have for how to implement these ideas?"

Oh.  Right.  With actual students.

I had a sudden flashback to when I was the department chair and not teaching any classes, but still expected to be the "instructional leader" for the department.  At that time, I felt like I was losing touch with what it meant to be in front of students, and it's one of the reasons I returned to the classroom.  Now, I've been away from the classroom again, and I'm surprised (and a little disappointed) that I'm sliding past thinking about the actual teaching experience.  Again.

It was good to have this reminder, not only as I prepare for this webinar, but also as I approach the end of my Fellowship and look forward to returning to the classroom in August.  All the content, strategies, and new ideas I have experienced won't go very far until I seriously consider what it all might look like, away from the sterile professional development environment and plopped down in the middle of a wonderfully personal, messy, and exciting classroom.

So I'm remembering using an individual to group to classroom discussion strategy for starting a Notice and Wonder routine.  I'm thinking about the different colored sticky notes for students to write their reflections and questions on.  And I'm reviewing all the checking for understanding routines I use to take the temperature of the class.  Since the upcoming webinar I'm giving is not specifically about this kind of stuff, and it's difficult to model some of these strategies in a remote situation, I have to think creatively about how to at least tell the story of how I've used them.

But that's the beauty of teaching for me -- figuring out how to tell the story of my subject in such a way that the students become part of that story.  Writing and presenting webinars about ways to tell the story continues to be fun.  But actually getting my hands, heart, and imagination in contact with students is something special.  It's far too easy to forget that (and too many people making decisions about education seem, like me, to forget).  

It was good to be reminded.

Image by Pexels from Pixabay

Dividing a Circle

I came across this item (https://www.loc.gov/resource/g3200m.gcw0013960/?sp=9) from an online copy of the 1862 Johnson's new illustrated family atlas.  The picture intrigued me for lots of reasons, but the one that stuck in my head was the fact that it shows a circle divided into nineteen equal sectors.  That's pretty remarkable, since the 360 degrees in a circle are not nicely divided into 19 equal pieces, and I did not think 19 pieces was one of the divisions possible using compass and straightedge constructions.  (I checked; it isn't.)

I wondered how the draftsperson who created the image divided the circle?  Protractors have been around for centuries, so it is possible that they simply measured the necessary angle with a protractor.  I wasn't satisfied with that, because it seems not quite precise enough.  One would need a really carefully scaled protractor to measure an angle of just under 18.95 degrees.  Maybe the draftsperson just used 19 degrees?  After all, 19 sectors at 19 degrees each would be 361 degrees, which at the scale of the drawing might have been accurate enough.  So maybe they did use a protractor.

But I wanted something precise and elegant.  Something that could be done simply, and would provide an accurate division of the circle, without losing even a fraction of a degree.  And if the process were scalable to divide the circle into any number of sectors, that would be the icing on the delicious mathematical cake.  I had not seen such a process or tool, but its existence seemed possible and even reasonable, even if not with a compass and straightedge.

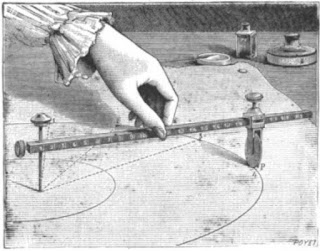
After some searching, I found an amazing device called ... get ready for it ... the Circle-Divider! (https://babel.hathitrust.org/cgi/pt?id=uiug.30112037739783&view=1up&seq=220&skin=2021).  The article in an 1885 issue of Scientific American Supplement even used 19 divisions as an example. 

The basic idea uses a small wheel with radius of one unit attached to the end of an adjustable arm, so that it could roll around the perimeter of a circle with radius n units.  (It doesn't matter what units we use, as long as they are the same for the wheel and the rotating arm.)  A mark would be positioned at the bottom of the wheel, and the arm would be rotated around the center of the radius n circle, with the wheel rolling along the perimeter.  Each time the mark on the wheel reaches the lowest point, you can mark that position on the circle, and after one rotation, the circle is divided into n sectors!  (And I love that the illustration shows what appears to be a woman's hand using the device.)

This was beautiful and simple!  All it uses is the formula for circumference, which middle school students typically know.  Since the circumference of the circle on the paper is 2pi times its radius, n, and the wheel has circumference 2pi, the wheel will rotate exactly n times as it rolls around the perimeter of the circle.  (And if your circle divider draws a 19-inch circle with 19 sectors, but you want a five-inch circle with 19 sectors, just make your smaller circle concentric with the larger one, and the sectors you want will match with the sectors you have.)

It's not a traditional compass and straightedge construction, but awfully close!  No need for a ruler (since you can construct a segment n units long, given the length of one unit).  The result is theoretically exact.  And the process is scalable to any size circle with any number of sectors!  This is what I consider a precise and elegant solution to the problem.

Here's the difficulty ... I have not been able to find this tool referenced anywhere but in this short Scientific American article about it.  And the only name I have is "circle-divider" from that article.  It's not part of a typical drafting toolkit, either modern or 19th century as far as I can tell.  A librarian from the Science, Technology, and Business Reading Room at the Library of Congress is helping me track it down, but neither of us has found another reference so far.

I'm not sure if I'm hoping to be able to find an actual circle-divider (I love old tools), or if I'm more excited to actually build one (I've got plenty of cardboard and other scraps around).  Either way, the circle-divider will certainly be making an appearance in my Trig/PreCalc class next year!